The following circuit has a voltage source that operates between 3V and 5V and is connected to the Op Amp’s positive input, across a resistor divider R2 and R1 at the node Va. The simulation is run for 200m secs.

The design is as following: applying super position

Following is the Spice file :  opamp_gnd

Video :Positive Feedback

 

 

 

 

 

 

LTspice IV is a high performance SPICE simulator, schematic capture and waveform viewer with enhancements and models.

The simulator software can be downloaded from the following link:

ltspice.linear-tech.com/software/LTspiceIV.exe

The following is a circuit on how to use a switch ” .model ” in simulations, it has been created for a RC circuit.

As seen these switches are not a physical model, they require a initial voltage to start to act as one.

20150820_switch_RC is the simulation file for the given circuit, can be seen by installing LtSpice.

 

 

Every switch has some instance of resistance when on or off;
Ron = 1            ‘ the resistance when the switch is turned on.’
Roff = 10meg   ‘ the resistance when the switch is turned off.’
Vt    = 0.1         ‘ the instance when the switch turns on’

Classical way to solve the RC filter in time domain :

RC filter classical time domain way

 

        The frequency and the sine wave was set by the function generator. The input, output wave forms were observed from the CRO. The conditions taken were  a 50KΩ , 1KΩ and a current source. The input was fed to the 2.1 speaker’s connector jack to produce the sound of the fed sine wave.

Frequency (Hz)	Input (peak to peak value)	Conditions	Output (Peak to peak value)	Observations
600	2 V	50 KΩ	0.2 V	Distorted wave
600	2 V	1 KΩ	2 mV	Small signal with distorted wave
600	2 V	Current Source	100 mV	Distorted wave
600	5.5 V	Current Source	300 mV	Not distorted
600	5.5 V	50 KΩ	100 mV	Partially distorted
600	5.5 V	1 KΩ	5 mV	Bottom of the wave distorted
450	11 V	1KΩ	8 mV	Distorted wave
450	11 V	50 KΩ	200 mV	Extremely distorted wave

From the tabulation the maximum output 300mV is achieved when the input is set to a peak to peak value of 5.5V connected from the current source (PNP BJT’s collector junction ).

To determine the amplification,

the voltage at the base of the NPN transistors is ≈ 2.5V. now divided by the resistance of resistor R6 gives us the current.

 now, the obtained current value multiplied by R5

gives the amplified output ≈ 5V.

 

• We wanted to use the transistor as an amplifier.
• The input voltage at the base was 3v.
• Two resistors, one at the emiiter(R1) and the other at the collector(aR1) were connected.
• 9v supply was given at R1.

Constraints :

• We wanted head room of 2v.
• We wanted to obtain maximum gain.

Design :

• Subtracting 0.7v at the emitter from 3v at the base we get 2.3v.
• Current across R1 is

• As we needed 2v head room, the voltage drop across aR1 needed to be 4.7v(ie, 4.7v+2.3v=7v) which is 2v lesser then 9v.
• Current across aR1 is

• The maximum gain we can get is a gain of 2.

• Hence the resistor value at the collector should be two times more than the one at the emitter.

• We wanted to use a transistor as a current source.
• Two resistors, one at the emiiter(R1) and the other at the collector(R2) were connected.
• A voltage divider circuit with a supply of 9v was connected at the base that could supply certain voltage.

Constraints :

• We wanted 4.5mA of current to pass through.
• 9v supply was given to the resistor at the emitter.

Design :

• The resistor at the collector(R2) was chosen as 1k based upon the resistance of the mic.
• We knew that the diode would turn on at around 0.7v.
• The voltage drop across R1 should be some resistance that gives 4.5mA of current.
• Depending upon the availability of the resistors, 330 ohms was chosen for R1, keeping the 9v supply in mind and voltage at emiiter, it was calculated that 1.5v drop would give us 4.5mA of current.
• Now from the voltage divider, a certain amount of voltage needed to be supplied so that the drop across R1 is 1.5v (ie, 9v – 7.5v)
• So we wanted 6.8v from the voltage divider (ie, 6.8v + 0.7v = 7.5v)
• Hence, the voltage divider circuit was designed with the following formula.

• The ratio of the scaling factor was approximately 3 and depending upon the availability of the resistors, R3 was taken as 4.7k and R4 was taken as 14.5k.

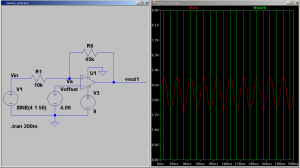
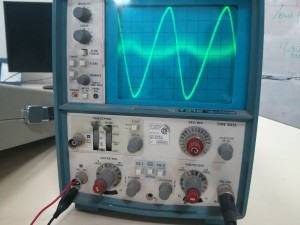
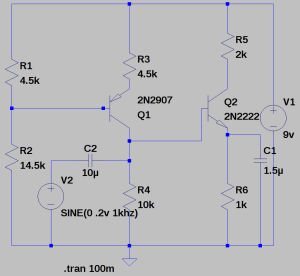
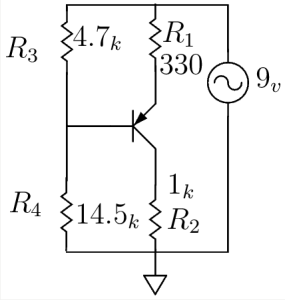
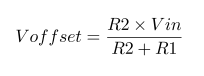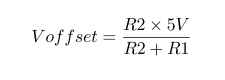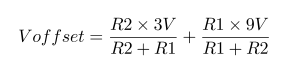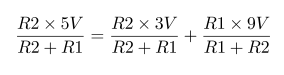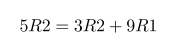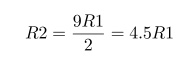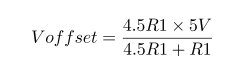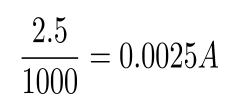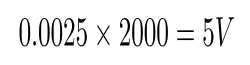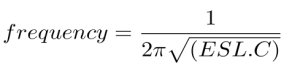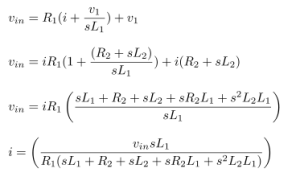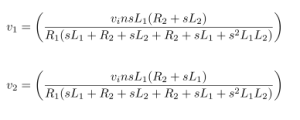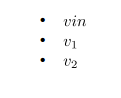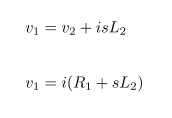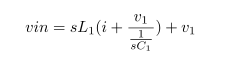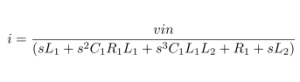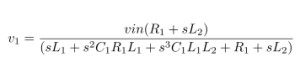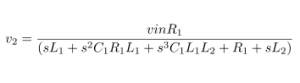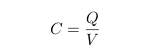Impedance of Various 100μF Capacitors :

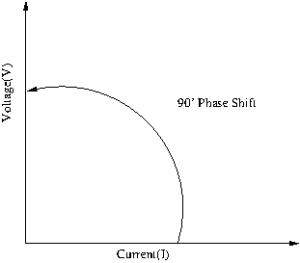
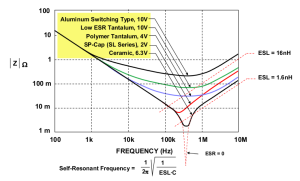
• The figure tells us that the impedance of a capacitor will decrease monotonically as frequency is increased.

• In actual practice, the ESR causes the impedance plot to flatten out.

• As we continue up in frequency, the impedance will start to rise due to the ESL of the capacitor.

• The location and width of the “knee” will vary with capacitor construction, dielectric and value.

• This is why we often see larger value capacitors paralleled with smaller values. The smaller value capacitor will typically have lower ESL and continue to “look” like a capacitor higher in frequency.

• This extends the overall performance of the parallel combination over a wider frequency range.

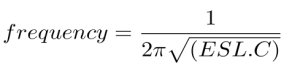
Reference : From Analog Devices Tutorial

Frequency Characteristics of a 0.1 uf Capacitor :

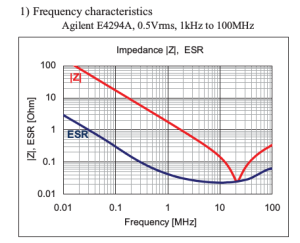
The impedance matches with ESR at around at around 2 Mhz.

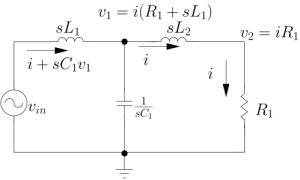
ESL Analysis :

Frequency = 20 Mhz

Capacitance = 0.1 uF

From the frequency equation , ESL = 0.63 nH

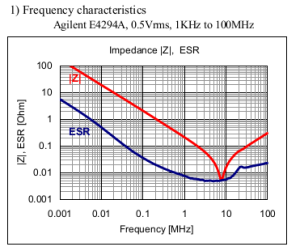
 Frequency Characteristics of a 1 uf Capacitor :

The impedance matches with ESR at around at around 8 Mhz.

ESL Analysis :

The impedance matches with ESR at around at around 8 Mhz.

Frequency = 8 Mhz

Capacitance = 1 uF

From the frequency equation , ESL = 0.39 nH

 

The impedance matches with ESR at around at around 2 Mhz.

ESL Analysis :

Frequency = 2 Mhz

Capacitance = 10 uF

From the frequency equation , ESL = 0.63 nH

Frequency Characteristics of a 10uf Capacitor :

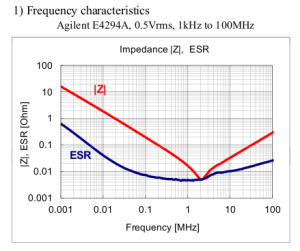
The impedance matches with ESR at around at around 2 Mhz.

ESL Analysis :

Frequency = 2 Mhz

Capacitance = 10 uF

From the frequency equation , ESL = 0.63 nH

Capacitor Graph Reference : Datasheets from Digikey

 

 

Assume a current ‘i’ flows in a particular direction.

The voltages at the nodes have been named as vin, v1,v2

At node v2 :

At node v1 :

Through SL1 :

At vin :

v1 and v2 in terms of vin :

 

Circuit Analysis pdf

let us take the above circuit into consideration, with three nodes namely:

and i is the current passing through them.

1. Considering node v2 :

2. Now at node v1 :

3. To determine vin :

4. The current i can written as :

5. v1 and v2 in terms of vin

 

 

 

PoweringUpLED pdf

Powering up an LED

ledcalc.com ; A useful tool to determine the value of resistors to be used in the circuit.

V = I × R (Ohm’s law)

supply voltage = 5V

resistor used = 2 x 33ohm resistor connected in parallel = 16.5 ohm

to determine current ; I = V / R

5 / 16.5 = 300mA

(Power supply voltage − LED voltage) / current (in amps) = desired resistor value (in ohms)

To calculate the amount of power that the resistor will dissipate;

Power Rule: P = (I × V ) W
If a current I flows through through a given element in your circuit, losing voltage V in the process, then the power dissipated by that circuit element is the product of that current and voltage: P = I × V.

Capacitor pdf

Capacitor

Information

A capacitor (originally known as a condenser) is a passive two-terminal electrical component used to store energy electro statically in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors (plates) separated by a dielectric (i.e. insulator). The conductors can be thin films, foils or sintered beads of metal or conductive electrolyte, etc. The “non-conducting” dielectric acts to increase the capacitor’s charge capacity. A dielectric can be glass, ceramic, plastic film, air, vacuum, paper, mica, oxide layer etc. Capacitors are widely used as parts of electrical circuits in many common electrical devices. Unlike a resistor, an ideal capacitor does not dissipate energy. Instead, a capacitor stores energy in the form of an electrostatic field between its plates.

When there is a potential difference across the conductors (e.g., when a capacitor is attached across a battery), an electric field develops across the dielectric, causing positive charge +Q to collect on one plate and negative charge −Q to collect on the other plate. If a battery has been attached to a capacitor for a sufficient amount of time, no current can flow through the capacitor. However, if a time-varying voltage is applied across the leads of the capacitor, a displacement current can flow.

 

 

 

 

 

Capacitors are widely used in electronic circuits for blocking direct current while allowing alternating current to pass. In analogue filter networks, they smooth the output of power supplies. In resonant circuits they tune radios to particular frequencies. In electric power transmission systems, they stabilize voltage and power flow.

An ideal capacitor is wholly characterized by a constant capacitance C, defined as the ratio of charge ±Q on each conductor to the voltage V between them