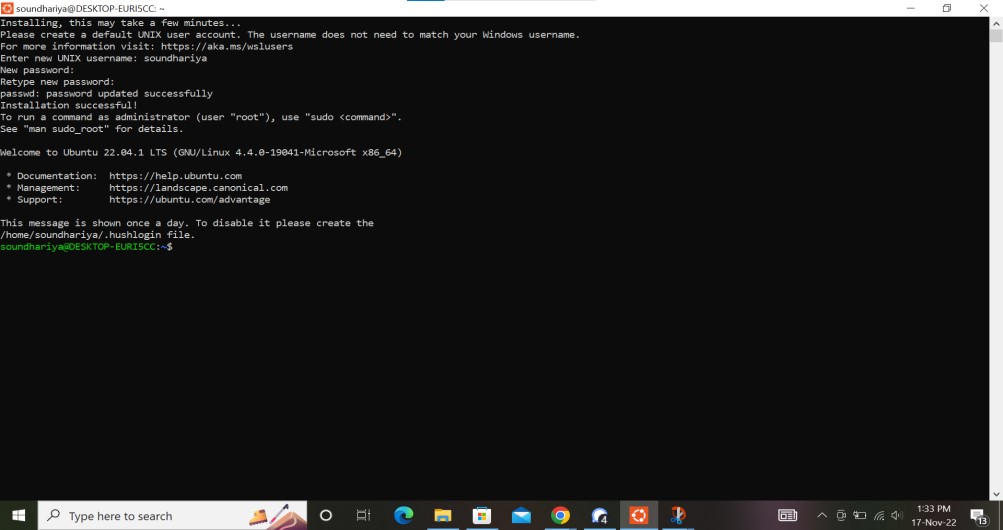
~ Soundhariya, Sandhiya.B
Trigonometric ratios are the ratios of the length of sides of a triangle. These ratios in trigonometry relate the ratio of sides of a right triangle to the respective angle. The basic trigonometric ratios are sin, cos, and tan, namely sine, cosine, and tangent ratios. The other important trig ratios, cosec, sec, and cot, can be derived using the sin, cos, and tan respectively. Using scratch, the visualization of trigonometric ratios is comprehendible.
Let us have a look at the right-angled triangle drawn using the scratch shown below. Trigonometric ratios can be used to determine the ratios of any two sides out of a total of three sides of a right-angled triangle in terms of the respective angles.
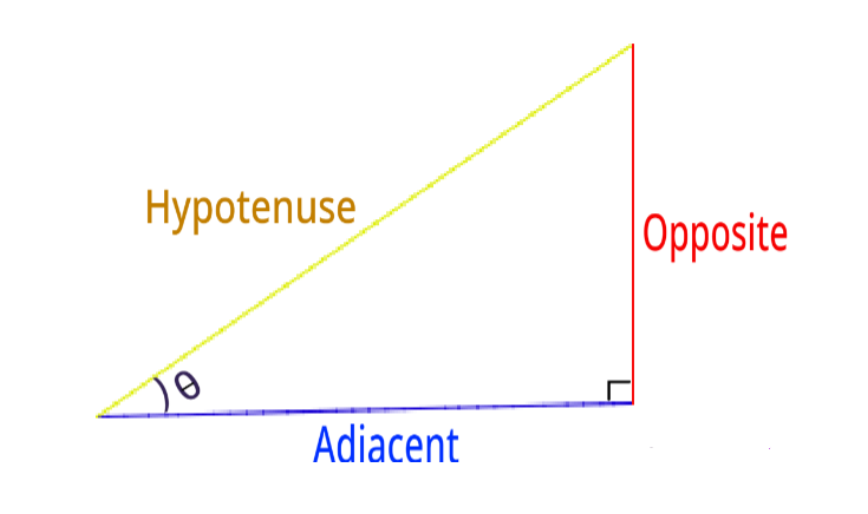
The values of these trigonometric ratios can be calculated using the measure of an acute angle, θ in the right-angled triangle given below. This implies that the value of the ratio of any two sides of the triangle here depends on the angle. We can alternatively find the values of these trig ratios. Also, only the base and perpendicular will interchange for the given right triangle in that case.
Concerning θ, the ratios of trigonometry are given:
Sine: Sine of an angle is defined as the ratio of the side opposite (perpendicular side) to that angle to the hypotenuse.
cosine: The cosine angle is defined as the ratio of the side adjacent to that angle to the hypotenuse.
Tangent: The tangent angle is defined as the ratio of the side opposite to that angle to the side adjacent to that angle.
Cosecant: Cosecant is a multiplicative inverse of sine.
Secant: Secant is a multiplicative inverse of cosine.
Cotangent: Cotangent is the multiplicative inverse of the tangent.
The above ratios are abbreviated as sin, cos, tan, cosec, sec, and tan respectively in the order they are described. So, for Δ ABC, the ratios are defined as:
sin θ = (Side opposite to θ)/(Hypotenuse) = AB/AC
cos θ = (Side adjacent to θ)/(Hypotenuse) = BC/AC
tan θ = (Side opposite to θ)/(Side adjacent to θ) = AB/BC = sin ∠C/cos ∠C
cosec θ = 1/sin θ = (Hypotenuse)/ (Side Opposite to θ) = AC/AB
sec θ = 1/cos θ = (Hypotenuse)/ (Side Opposite to θ) = AC/BC
cot θ = 1/tan θ = (Side adjacent to θ)/(Side opposite to θ)= BC/AB

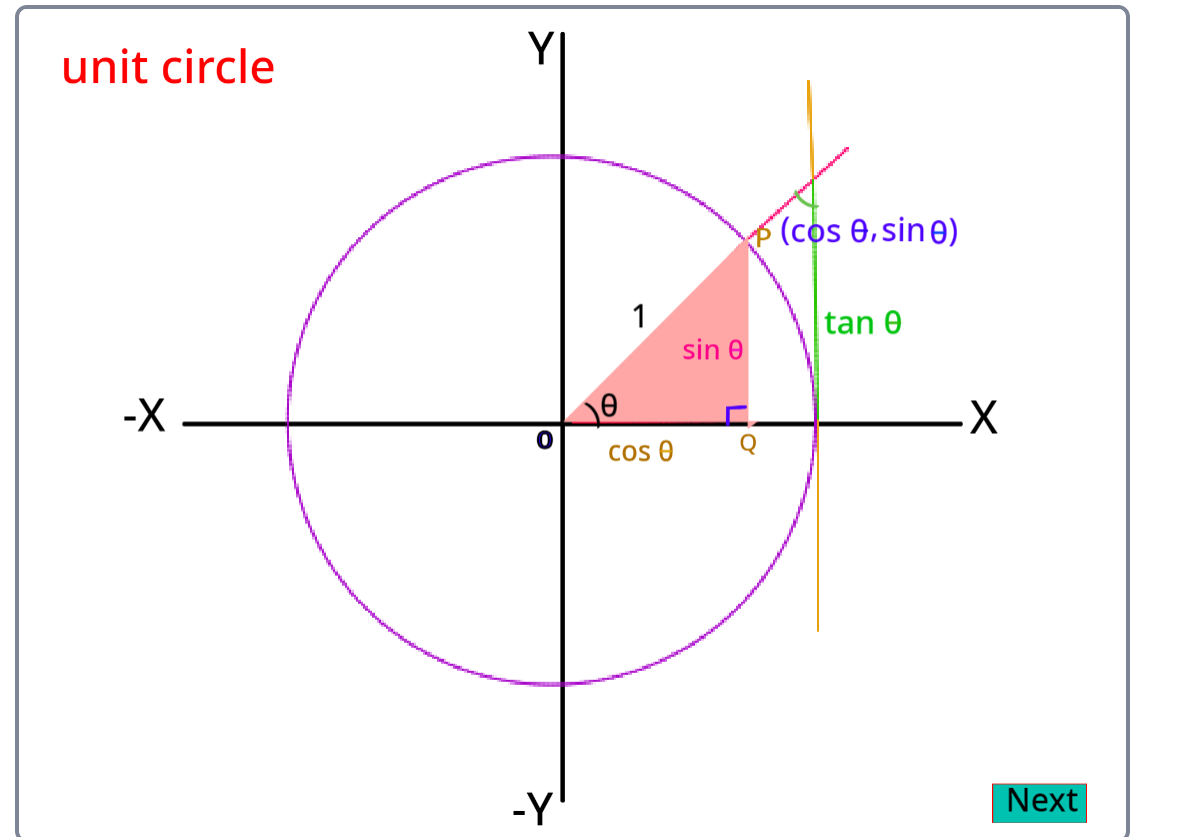
Unit Circle and Trigonometric Values:
Unit circles can be used to calculate the values of basic trigonometric functions- sine, cosine, and tangent. The following diagram shows how trigonometric ratios can be represented in a unit circle.
Degrees to radians:
In geometry, both degree and radian represent the measure of an angle. One complete anticlockwise revolution can be represented by 2π (in radians) or 360° (in degrees). Therefore, degree and radian can be equated as:
2π = 360° And π = 180°
Hence, from the above equation, we can say, 180 degrees is equal to π radian.
Usually, in general geometry, we consider the measure of the angle in degrees (°). Radian is commonly considered while measuring the angles of trigonometric functions or periodic functions. Radians are always represented in terms of pi, where the value of pi is equal to 22/7 or 3.14.
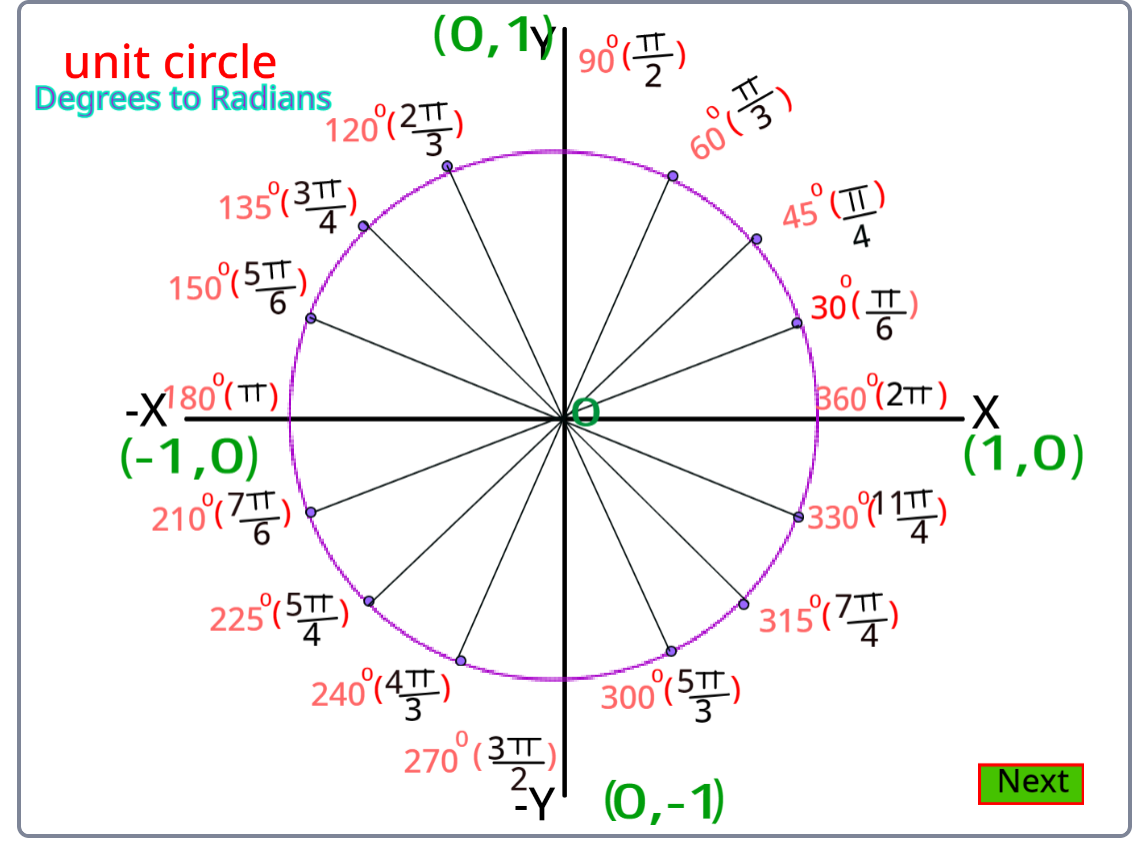
Trigonometric ratios of some special angles:
In the trigonometric ratios table, we use the values of trigonometric ratios for standard angles 0°, 30°, 45°, 60°, and 90º. It is easy to predict the values of the table and to use the table as a reference to calculate values of trigonometric ratios for various other angles, using the trigonometric ratio formulas for existing patterns within trigonometric ratios and even between angles. The trigonometric ratios of 45° using scratch are shown below.

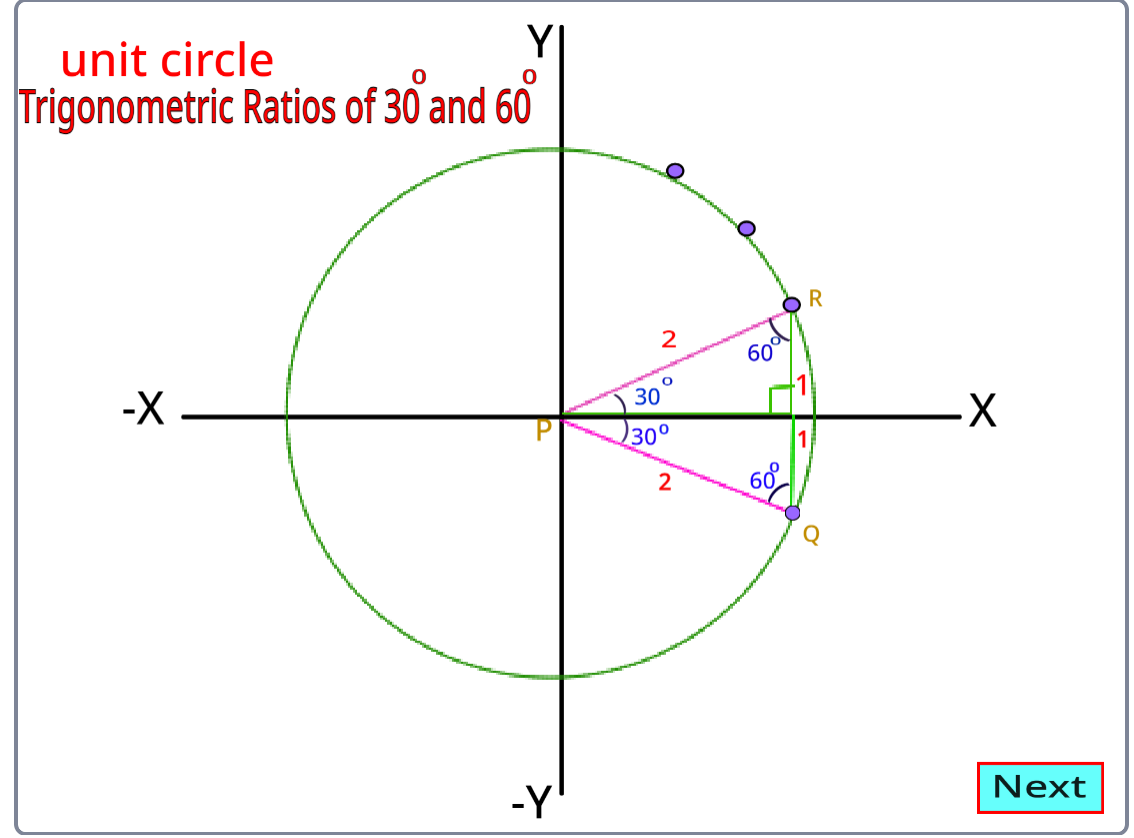
In right Δ PQR, if ∠P and ∠Q are assumed as 30° and 60°, then there can be infinite right triangles with those specifications but all the ratios written above for ∠P in all of those triangles will be the same. So, all the ratios for any of the acute angles (either ∠P or ∠Q) will be the same for every right triangle. This means that the ratios are independent of the lengths of the sides of the triangle.
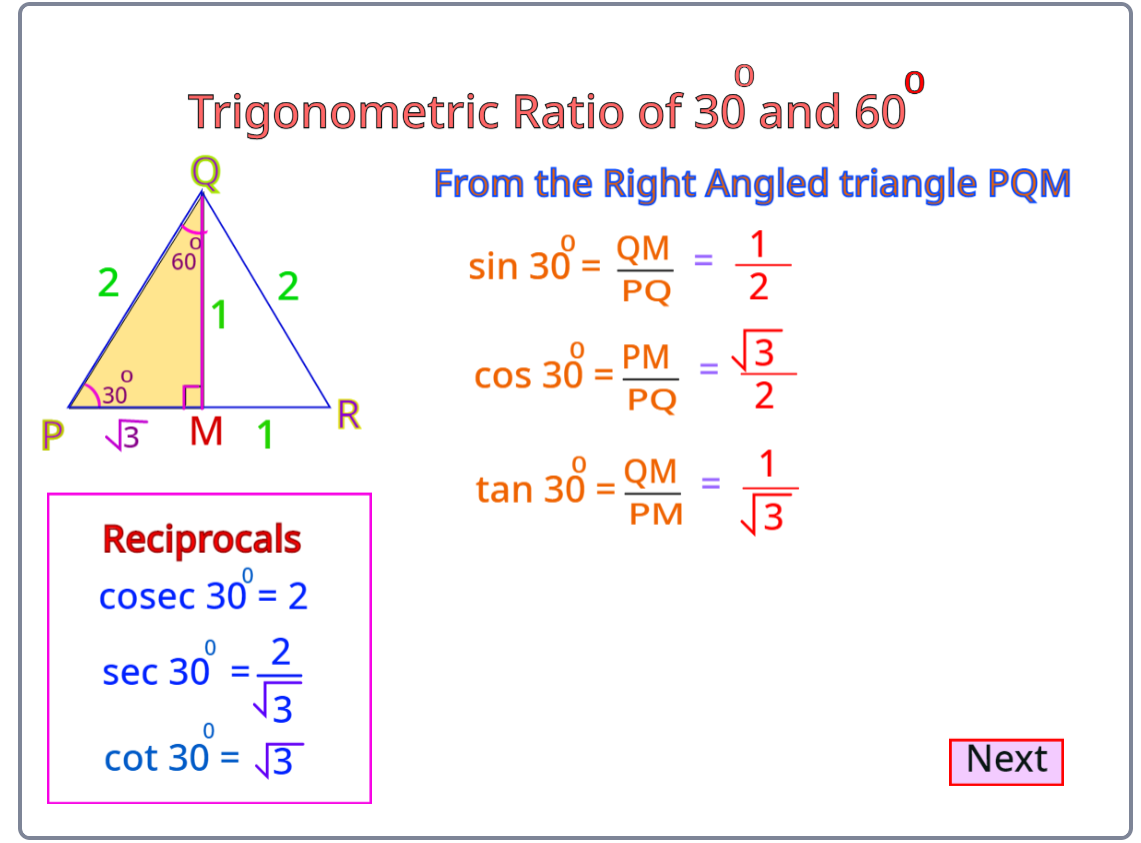
The trigonometric ratios of 30° and 60°simulated using the scratch program are shown below.
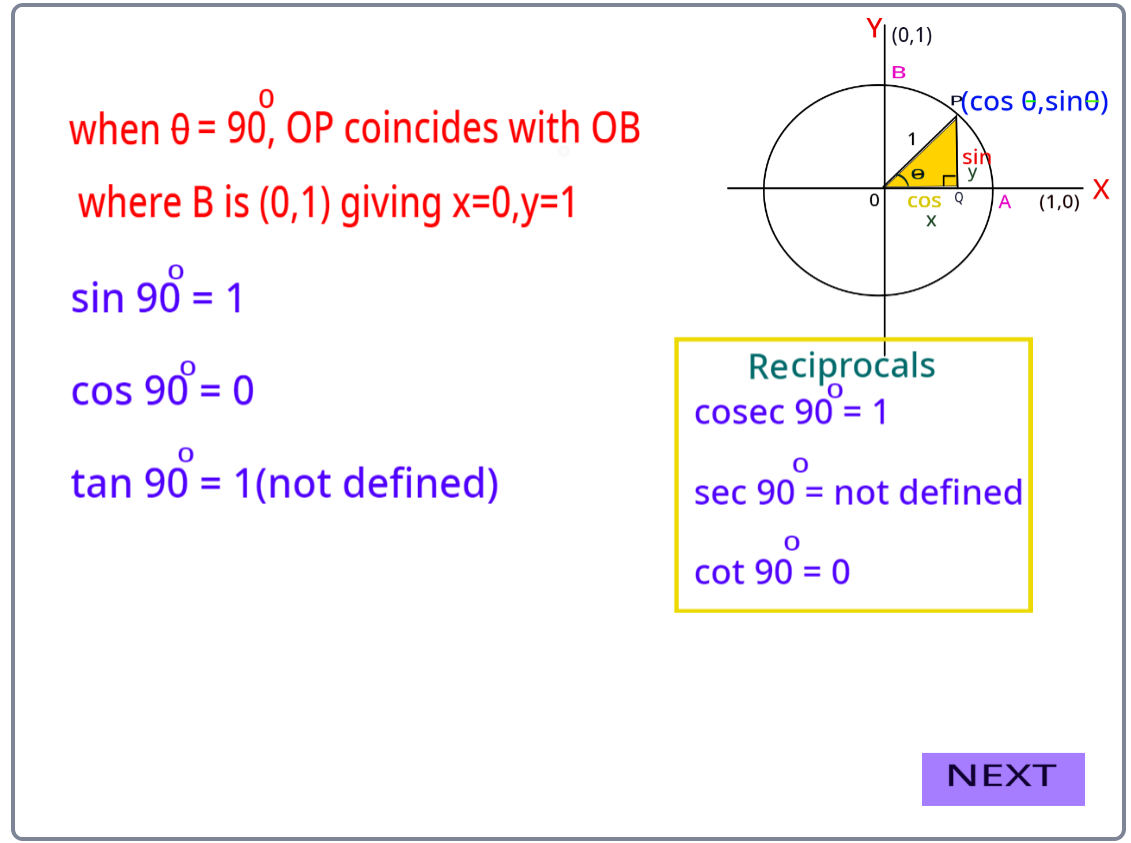
The trigonometric ratios of 90° and 0° using scratch programming are shown below.

Trigonometrical Ratios of 0 degrees are commonly called standard angles and the trigonometrical ratios of these angles are frequently used to solve particular angles. In ∆ABC is a right-angled triangle. If the length of the side BC is continuously decreased, then the value of ∠A will keep on decreasing. Similarly, the value of ∠C is increasing as the length of BC is decreasing. When BC = 0, ∠A = 0 , ∠C = 90° and AB = AC.
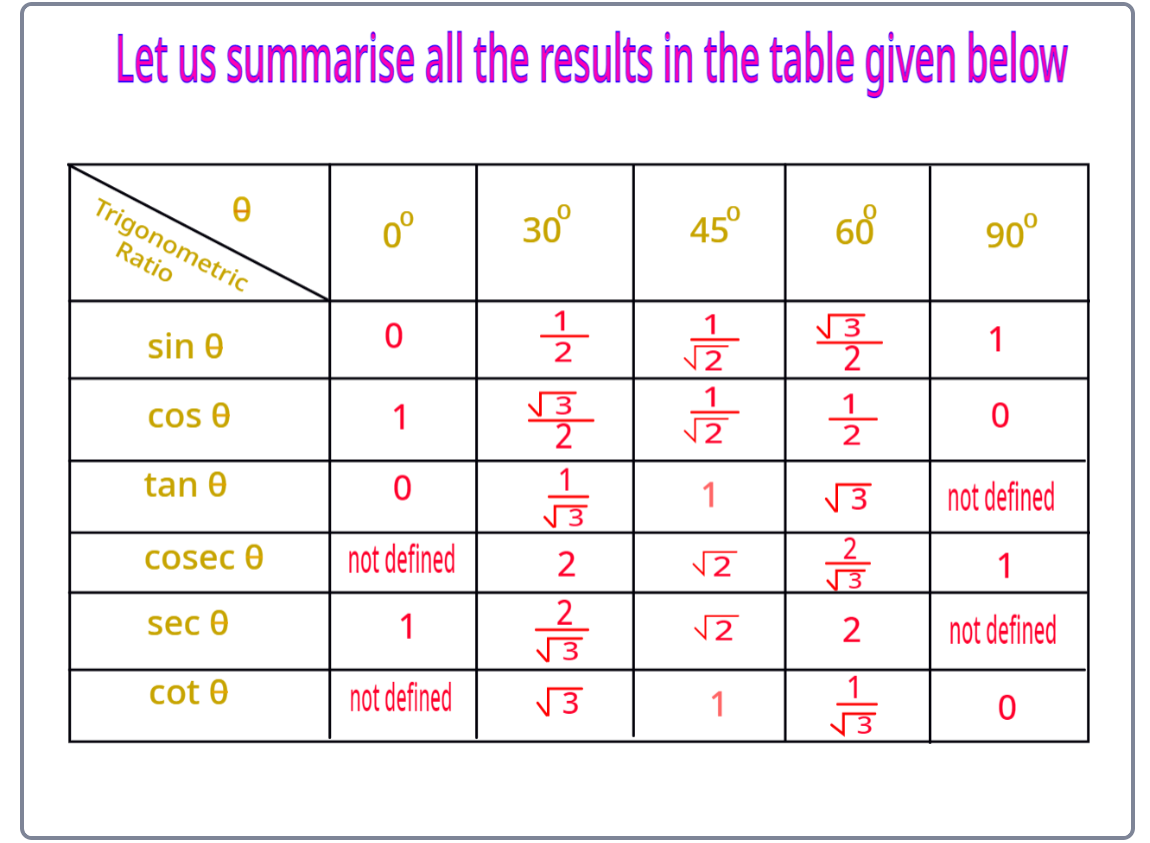
Trigonometric Ratios Table:
Attached the scratch link: https://scratch.mit.edu/projects/754205615
The summarization of the value of trigonometric ratios for specific angles is in the table below:
Some of the applications of trigonometric ratios are:
- Measuring the heights of towers or big mountains
- Determining the distance of the shore from the sea
- Finding the distance between two celestial bodies
- Determining the power output of solar cell panels at different inclinations
- Representing different physical quantities such as mechanical waves, electromagnetic waves, etc.