UNDERSTANDING ALIASING AND SAMPLING USING PYTHON

~Bakyalakshmi

Sampling theorem:

fs≥2fm

• A continuous time signal can be represented as samples and can be recovered back when sampling frequency f_s is greater than or equal to twice the highest frequency component of message signal.
• If this condition does not satisfy, it leads to aliasing.
• Aliasing is an effect   that causes different signals to become indistinguishable when sampled.

Visualizing using python:

import matplotlib.pyplot as plt #  to plot

import numpy as np

#numerical python to get array of float values and for sine operation

t = np.arange(0, 2e-3, 10e-6) # x axis time period

# sampling at fs =10kHz in time domain ts=1/fs (0.1ms)

ts = np.arange(0,2e-3,0.1e-3)

f = 1000 # message signal fm

b = np.sin(2*np.pi*f*t) #phase for sinewave

c = np.sin(2*np.pi*f*ts)

plt.plot(t,b,”g”) # plot of message signal (1kHz)

plt.plot(ts,c,”k*”) # plot of sampled message signal (1kHz)

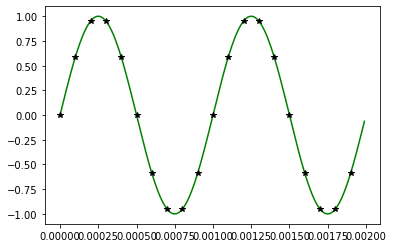
fs>=2fm:      Input frequency= 1kHz          sampling frequency = 10kHz

f=9000

b = -np.sin(2*np.pi*f*t)

c = -np.sin(2*np.pi*f*ts)

plt.plot(t,b) # plot of message signal (9kHz)

plt.plot(ts,c,’r+’)  # plot of sampled message signal (9kHz)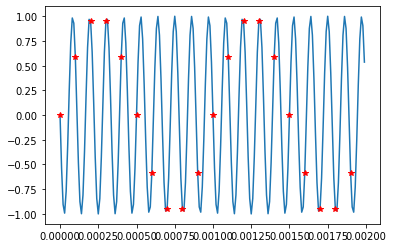

fs<2fm:      Input frequency = 9kHz        sampling frequency = 10kHz

Sampled output of 1kHz and 9kHz :

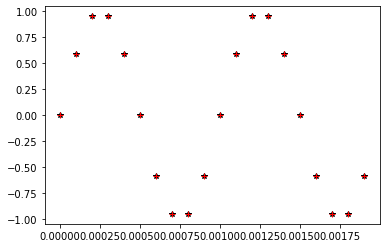
Aliasing of 1kHz and 9kHz

part1: https://youtu.be/og-Pn2oOqP4