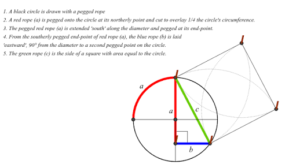
BHARATHA TIRTHA II- International conference on Indian knowledge systems was organized by IIT Kharagpur. Dr. Sanjeev Ranganathan, founder of STEMLAND was invited to present and he presented on the topic of Rajju ganit (string geometry, cord geometry).
He demonstrated briefly the concept of squaring the circle can be done using the Rajju ganit method. Using the rope, a circle, and a square of the same area can be constructed and observed.
There are two main new features:
(1) The cord replaces the entire compass box.
(2) Empirical methods are admitted in geometry contrary to the philosophy of formal math and using instead the philosophy of approximation.
Some other interesting topics that were presented at the conference were trigonometry in Ancient India and how that led to many discoveries and applications.
Jyotpatti: Trignometry in India
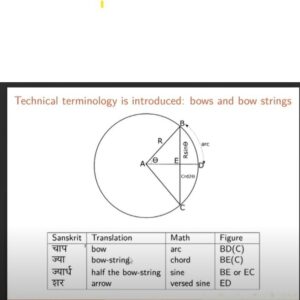
Trigonometry in India is called Jyotpatti.” Ja” means chord in a circle and “Jia” means string in a bow. Mathematicians used this to find the relation between the arc of a circle and the chord of a circle. The sine function is ubiquitous in all disciplines. It is very important to study the application part of sine and cosine functions.
Bhaskara’s metaphor for sine and cosine:
Bhaskar Acharya is a 12th-century astronomer and mathematician. He brought in the importance of science in astronomy, and the application of it is beautifully brought out with a nice simile.
He says that,
Just as fabric(pata)is made up of crisscrossed threads Likewise the spherics or science of astronomy is crisscrossed with sine and cosine functions.
Sines and cosines are everywhere in astronomy:
Interestingly, sines and cosines from the earliest times were formally a part of astronomy rather than a separate discipline of mathematics, it is because applications in astronomy fall all over the place.
The main phenomenal applications such as
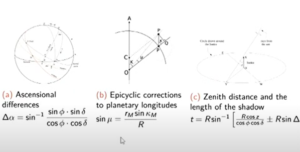
- Ascensional differences between planets. (Spherical trigonometry)
- Epicyclic orbital corrections to planetary longitudes.
- Zenith distances and the length of the shadows.
Arcs and chords: The origins of trigonometry in India:
In the 17th century, a famous mathematician named Nityananda Sarvasisiddhantaraja explicitly links the advantage of looking at half chords.
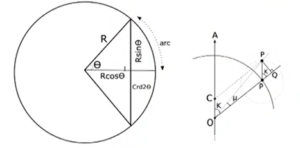
Mathematicians paid more attention to what a chord concerning a given arc is, What is half of the chord of double the arc, and the right-angled triangle which is used for mathematics and computes various line segments concerning half of the chord made computations much easier for astronomers.
Technical terminology introduced bow and bow string:
The evolution of trigonometry in India:
Practitioners needed to compute:
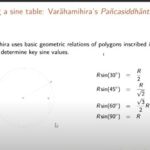
- Half chords and other line segments in right triangles using the geometry of polygons inscribed in a circle.
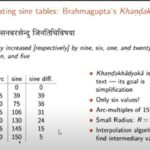
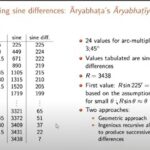
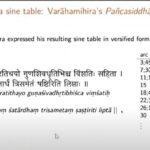
- Tables of Rsines are computed for various values of R.
- Linear(or occasionally second-order) interpolation is used to determine non-tabulated values.
Addressing these led to brilliant discoveries and the results from the middle.
Mathematicians like Brahmagupta, Aryabhatta, and Varahamihra have given the tables of sine and their geometric dimensions of it.