An arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant.
For example, the series of natural numbers: 1, 2, 3, 4, 5, 6… is an Arithmetic Progression, which has a common difference between two successive terms equal to 1 (2 -1). Even in the case of odd numbers and even numbers, we can see the common difference between two successive terms will be equal to 2.
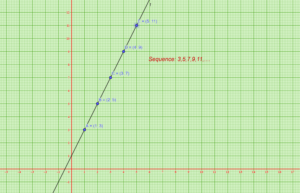
This can be observed visually using a graph. If an arithmetic sequence is plotted in a graph lies on a straight line. There is a finite distance between points.
For plotting in a graph, the sequence is written as in the following table.
Sequence of numbers: 3,5,7,9, 11, …
|
Term(x)
|
Number of squares(y)
|
Point(x,y)
|
Formula /Pattern
|
|
1
|
3
|
(1,3)
|
3=2(1-1) +3
|
|
2
|
5
|
(2,5)
|
5=2(2-1) +3
|
|
3
|
7
|
(3,7)
|
7=2(3-1) +3
|
|
4
|
9
|
(4,9)
|
9=2(4-1) +3
|
|
5
|
11
|
(5,11)
|
11=2(5-1) +3
|
|
6
|
13
|
(6,13)
|
13=2(6-1) +3
|
|
7
|
15
|
(7,15)
|
15=2(7-1) +3
|
|
.
|
.
|
.
|
.
|
|
.
|
.
|
.
|
.
|
|
n
|
.
|
.
|
tn=a+(n-1) d
|
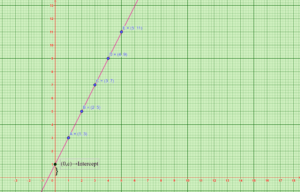
The plotted point of an AP is shown below:
Notations in Arithmetic Progression:
In AP, we will come across some main terms, which are denoted as:
- First-term (a)
- Common difference (d)
- nth term. (an)
First Term of AP
The AP can also be written in terms of common differences, as follows;
where “a” is the first term of the progression.
a, a + d, a + 2d, a + 3d, a + 4d, ………., a + (n – 1) d
Common Difference in Arithmetic Progression
Suppose, a1, a2, a3, ……………. is an AP, then the common difference “d” can be obtained as;
d = a2 – a1 = a3 – a2 = ……. = an – an – 1
Where “d” is a common difference. It can be positive, negative, or zero.
The nth term of an AP
The formula for finding the n-th term of an AP is:
an = a + (n − 1) × d
where
a = First term
d = Common difference
n = number of terms
an = nth term
In the graph, the slope of the line formed by the arithmetic progression is equal to the common difference in Arithmetic progression.
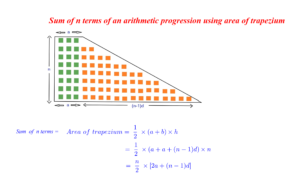
Sum of n terms of an arithmetic progression:
The sum of n terms of an AP can be easily found using a simple formula which says that, if we have an AP whose first term is a and the common difference is d, then the formula of the sum of n terms of the AP is
Sn = n/2 [2a + (n-1) d]
The proof of the sum of n terms can be visualized and derived using the area concept. This can be implemented and observed in GeoGebra.
Suppose we arrange the terms in the AP as shown in the figure we can calculate the area to find the sum of the first n terms in an AP.
This is can be done in two methods:
1.Using the area of the trapezium
2.Using the area of the rectangle.
1. Using the area of the trapezium:
When the terms in the AP are arranged as shown in the figure we can observe that it forms a trapezium. to find the sum of the first n terms in an AP the area of the trapezium can be calculated which gives the result of the sum of the first n terms.
2. Using the area of the rectangle:
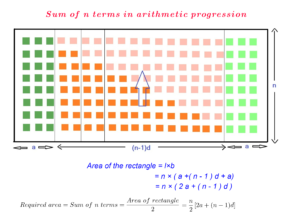
Likewise, the terms in the AP can be arranged in such a way that the tilted arrangement and the regular arrangement of the terms form a rectangle as shown in the figure. To find the sum of the first n terms in an AP the total area of the rectangle can be calculated and divided into half to get the required area which gives the result of the sum of the first n terms.
Finding the equation of a line using the arithmetic progression:
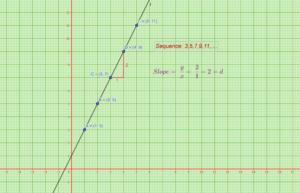
Lets take the sequence 3,5,7,9,11…..The nth term is taken as x and its number of squares as y.
As we know tn can be expressed as tn=a+(n-1)d.
i.e., y=tn=a+(n-1)d
We know that a=3,common difference is 2. Substituting we get
y=3+(x-1)2
y=3+2x-2
y=2x+1 ———- > Equation of the line.
General equation of a line is y=mx+c.
Here we can observe that m= slope =2 = common difference.
c=1 = Intercept (A point at which the given line cuts the y axis).
In an arithmetic progression intercept means the value of sequence, when x=0.
This can be observed in the graph given below.
+