C3STREAM Land Designs – Page 51 – (formerly Aura Auro Design)

July 8, 2017

Software to track students learning plan

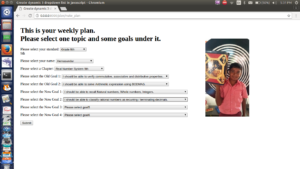
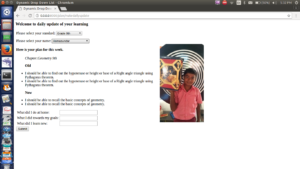
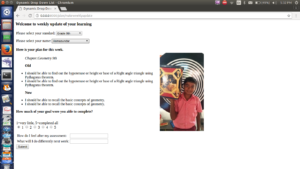
Pratap and myself were working on a project to create a software which tracks the students learning plan. We did it in Django. Before students were filling their daily plan and weekly plan in an excel sheet. Typing in it was difficult for them and took much more time to fill it. So we thought this software would be much easier for them. This software contains weekly plan, daily update and weekly update. They can select their standard and name. Once they select their name their picture with things that they liked most in STEM Land will appear. In weekly update they select their goals for the week, in Daily update they select their plan for that day and in weekly update they say how much they were able to complete their goal and what will they do different in next week. Through this software they come to know where they are and how they utilized the time and where to improve. We showed the project to the student and the were really happy to see it and did their plans within few minutes.

July 8, 2017July 15, 2017

Activity class in Isai Ambalam school

On Wednesday children had a sleepover in the school. On that day there was a power cut . Children didn’t bring their torch from their home. It was very dark and we had only one torch. They managed with that torch for that day. At that time students wanted to make a torch in the STEM land. Next day they brought water bottle and they wanted to do it. We started doing and through this process they came to know about the function of a resistor , battery and LED. Finally they built it and they will use it whenever they sleepover in the school.

July 3, 2017

Math with the 4th graders at Isaiamabalam school

The children worked on the process of adding two numbers in order to make split at the total to 10 + the remainder. The children used to Abacus to visually see the two numbers and its remainder. Then they paired up with their colleague and started practicing.

July 1, 2017July 1, 2017

Learning division

Children felt very difficult to understand what division is and why we do it. They were been explained with the fraction kit using the test tubes and the colourful beads. Using the fraction kit they learnt to divide things to number of people and was easy for them to understand the concept of division and where we apply it. They learnt division so easily by playing with the kit and were enjoying while learning it.

July 1, 2017

Visit to the Science Exhibition Express on Climate Change

We from Isai Ambalam School made a visit to the Science Exhibition Express on ‘Climate Change’ that arrived in Pondicherry. We took the children from 3rd grade to 7th grade from Isai and 10th graders of Udavi School also joined along. Most of the teachers also came along. Every STEM Land – AAD person were assigned 4 children so that they could discuss and explain about the things they are seeing in the exhibition. Each group was supposed to have a Udavi child and atleast a girl so that the group is balanced and diverse. In our group we learned about effects, causes and adaptation methods of climate change. It was very interesting for myself and my group as we all learned new things that day!

The group pic including all the children from Isai and Udavi and teachers and coordinators of Isai Ambalam School

July 1, 2017

Painting the clay room – Sat School

The clay room before we started to paint

Naveen and I took the help of the 4th graders to paint the clay room we are setting up in Isai Ambalam School. We scrapped the inner side walls of the room so that all the loose particles/paint came out. We then mixed white cement with water to cover the places where there were holes and black marks. Then we started painting the side walls. The children took a certain portion of the wall to paint(depending upon the height). Some also took a complete wall for themselevs to paint. Initially the children were worried that they would get paint in their hand/body. But once they took the paint brush in their hand, they were quite involved and didn’t woory much as would wash away everything in the end!

July 1, 2017

Hot Air Balloon

We made a big hot air balloon. We already completed making the balloon along with the 5^th graders. Today for the Saturday’s class we decided to make it fly.

We got some old cloth and some kerosene to get hot air from the fire. We lighted it up and held the balloon on top to get hot air going in. The balloon was a big spherical structure. We waited for a long time and couldn’t get the balloon filled with hot air.

Then we discussed with the children on why the balloon did not go up. Their assumptions were

The Balloon had holes in the structure.
Hot air did not go inside.
The balloon was too heavy. (We weighed the weight of the balloon and it was 206 g)
The balloon was not properly made.

Then we decided to make a small balloon and check if it was flying. This time we made a cuboid balloon structure whose height was around 50 cm high. Again with a lot of excitement we filled the balloon with hot air. We waited and waited but it could not go up. We still don’t know the reason why the balloon did not rise up???

All children excitingly seeing the hot air balloon

Holding fire and balloon on to top to fill hot air inside the balloon

We are waiting to see one go up.

June 26, 2017

Addition/Subtraction with 3rd graders

The 3rd graders demonstrated their addition and subtraction stories that they written last week using the Dienes Blocks. Initially, the children were confused with the words addition and subtraction. They were doing subtraction instead of addition. After some more practice they were able to do well.

June 26, 2017June 26, 2017

Unit conversion

Along with the 6th and 7th in Isaiambalam school, we wanted to estimate how far one Km would be. All the students made a guess and wrote down their check point on a route from their class.

The children wrote down how far their guess was compared to a Km, and took other nine checkpoints of other children, when they went back to class they decided to convert each checkpoint to meters, decameters, and hectometers.

June 24, 2017

Seeds and Seeds

This week 5th Graders studied Seeds and Seeds lesson from their curriculum and completed half of their lesson. They were excited about planting seeds in the school. So we decided to plant Chik Peas, Moong Bean and Mustard and kept under observation.